As primeiras teorias matemáticas da acústica incidem na frequência de vibração das cordas tensas, sendo Brook Taylor (1685-1731) – o criador das famosas séries com o seu nome – o primeiro a deduzir uma expressão analítica, para determinação da frequência de vibração das cordas tensas, em função do seu comprimento, tensão e densidade linear, a qual concordava com as leis experimentais de Mersenne e Galileo. O trabalho de Taylor foi publicado em 1713, tendo sido posteriormente aperfeiçoado e generalizado, mediante a introdução de derivadas parciais, por Daniel Bernoulli (1700-1782), Leonard Euler (1707-1783) e Jean le Rond d’Alembert (1717-1783). Considera-se que d’Alembert foi o primeiro a deduzir, em 1747, para o caso das cordas vibrantes, a equação diferencial da propagação ondulatória, actualmente denominada simplesmente por Equação de Onda.
Entretanto, Sauveur, por volta de 1700, observa que uma corda tensa pode vibrar de forma a que certos pontos da corda não oscilem, os quais denominou por nódos, e que certos pontos sofram uma oscilação muito violenta, os quais denominou por ventres. Facilmente reconheceu que esse tipo de vibração se devia à ocorrência de frequências superiores à frequência de vibração da corda como um todo, e verificou que as frequências mais altas eram múltiplas inteiras da frequência mais baixa, correspondente à vibração da corda como um todo, a qual denominou por Frequência Fundamental. Sauver denominou o conjunto de todas essas frequências por Harmônicos, correspondendo o 1º harmônico à frequência fundamental. Tal denominação é ainda utilizada atualmente.
Em 1755, Daniel Bernoulli demonstra teoricamente que é possível uma corda tensa vibrar de forma que estejam presentes, simultaneamente, vários harmônicos, sendo o deslocamento, de um dado ponto da corda, igual ao resultado da soma algébrica dos deslocamentos correspondentes a cada harmônico. Tal formulação ficou conhecida por Principio da Sobreposição.Em termos musicais, as harmônicas são componentes de um tom harmônico cujo som é multiplicado por um numero inteiro, ou adicionado com uma nota tocada em um instrumento musical. Os múltiplos não-inteiros são chamados de parciais ou sobretons. A amplitude e o posicionalmento das harmônicas e parciais que conferem timbres diferentes para os instrumentos (apesar de não serem comumente detectados por um ouvido humano não treinado), e são as trajetórias separadas dos sobretons de dois instrumentos tocados em um intervalo que permitem a percepção de seus sons como separados. Os sinos possuem parciais perceptíveis mais claramente do que a maioria dos instrumentos.
Um sobretom é um parcial (uma onda parcial ou uma frequência constituinte) que pode ser tanto harmônico como "inarmônico".
Um harmônico é um múltiplo inteiro da frequência fundamental. Um sobretom inarmônico é um múltiplo não inteiro da frequência fundamental.
Um exemplo de sobretons harmônicos: (harmonia absoluta)
| f | 440 Hz | tom fundamental | primeiro harmônico |
| 2f | 880 Hz | primeiro sobretom | segundo harmônico |
| 3f | 1320 Hz | segundo sobretom | terceiro harmônico |
| 4f | 1760 Hz | terceiro sobretom | quarto harmônico... |
Nem todos os sobretons são necessariamente harmônicos isto é, múltiplos exatos da frequência fundamental. Alguns instrumentos musicais produzem sobretons que são ligeiramente mais sustenidos ou bemolizados do que os harmônicos verdadeiros. A sustenização, ou bemolização, dos sobretons é um dos elementos que contribuem para seus sons ímpares e também tem como efeito tornar não periódicas suas formas de onda.
Alguns instrumentos como o diapasão ou as flautas produzem um som claro, quase perfeito, porque seus sobretons estão bastante próximos da harmonia absoluta com a frequência básica.
Em muitos instrumentos musicais, é possível se produzir as harmônicas superiores sem a nota fundamental estar presente. Em uma caso simples (como em uma flauta doce), isto tem o efeito de elevar a nota em uma oitava; porém em casos mais complexos outras variações também podem ocorrer. Em alguns casos isto também modifica o timbre da nota. Este é parte do método normal para a obtenção de notas mais altas nos instrumentos de sopro. A técnica estendida inclui algumas técnicas não-convencionais de tocar multifônicas que também geram harmônicas adicionais.
Nos instrumentos de corda é possível a produção de notas muito puras, chamadas de harmônicas pelos músicos, as quais possuem uma alta qualidade, assim como uma alta intensidade, localizada no "nó'' das cordas.
Série Harmônica
A série harmônica é uma série infinita, composta de ondas senoidais com todas as freqüências múltiplas inteiras da freqüência fundamental. Tecnicamente, a freqüência fundamental é o primeiro harmônico, no entanto, devido a divergências de nomenclatura, alguns textos apresentam a freqüência 2F como sendo o primeiro harmônico. Para evitar ambigüidades, consideramos, no âmbito desse artigo, que a fundamental corresponde ao primeiro harmônico. Não existe uma única série harmônica, mas sim uma série diferente para cada freqüência fundamental. A Tabela abaixo mostra dois exemplos de série harmonica. Uma se inicia no Lá1(110 Hz) e a outra no Do1(132 Hz). A freqüência dá nota Do1 foi arredondada para simplificar a tabela. Em um sistema temperado as freqüências das notas seriam ligeiramente diferentes (Ver observações e o texto abaixo). São mostrados os 16 primeiros harmônicos para cada série.
| # | Lá1 | Do1 | Observações | ||
|---|---|---|---|---|---|
| Nota | Frequência(Hz) | Nota | Frequência(Hz) | ||
| 1(F) | Lá1 | 110 | Do2 | 131 | Freqüência fundamental. Tecnicamente o primeiro harmônico. |
| 2 | Lá2 | 220 | Do3 | 262 | Uma oitava acima da fundamental. 2º harmônico |
| 3 | Mi3 | 330 | Sol3 | 393 | Uma quinta acima do 2º harmônico. |
| 4 | Lá3 | 440 | Do4 | 524 | Duas oitavas acima da fundamental. |
| 5 | Do#4 | 550 | Mi4 | 655 | Todos os harmônicos ímpares subseqüentes soam desafinados em relação aos equivalentes temperados |
| 6 | Mi4 | 660 | Sol4 | 786 | Note que o Sol4 da série de Do é diferente da mesma nota na série de Lá (linha abaixo) |
| 7 | Sol4 | 770 | Sib4 | 917 | |
| 8 | Lá4 | 880 | Do5 | 1048 | Três oitavas acima da fundamental |
| 9 | Si4 | 990 | Ré5 | 1179 | |
| 10 | Do#5 | 1100 | Mi5 | 1310 | |
| 11 | Ré#5 | 1210 | Fa#5 | 1441 | |
| 12 | Mi5 | 1320 | Sol5 | 1572 | |
| 13 | Fá#5 | 1430 | Lá5 | 1703 | Veja que o Lá 5 é muito desafinado em relação à mesma nota na série de Lá (última linha) |
| 14 | Sol5 | 1540 | Sib5 | 1834 | Estas notas não pertencem a nenhuma escala ocidental por terem intervalo inferior a um semitom. |
| 15 | Sol#5 | 1650 | Si5 | 1965 | |
| 16 | Lá5 | 1760 | Do6 | 2096 | Quatro oitavas acima da fundamental |
A partitura abaixo mostra as 16 primeiras notas da série iniciada em Do2, mostrada na tabela acima.
Harmônicos Naturais
No baixo, se tocarmos uma corda com um dedo da mão direita enquanto tocamos levemente (sem pressionar) com um dedo da mão esquerda nessa corda em determinados trastes (correspondendo aos nodos harmônicos, lugares em que não há movimento no padrão de oscilação), podemos ouvir distintamente o harmônico correspondente, porque os outros harmônicos assim são eliminados ou, pelo menos, a sua intensidade é consideravelmente diminuída.
Harmônicos ArtificiaisOs Harmônicos Artificias podem ser feitos com qualquer nota do braço. Você precisa pressionar uma nota com um dedo da mão esquerda, enquanto toca com o dedo indicador da mão direita, econstando o polegar levemente sobre a corda (no estilo Jaco Pastorius), ou tocando a nota com o dedo médio, ou anelar e encostando o indicador (estilo Steve Bailey).
Jaco Pastorius com weather Report - Birdland
Steve Bailey - Masterclass

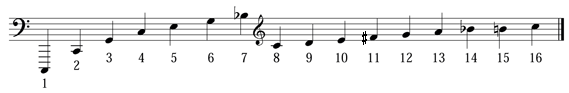



Nenhum comentário:
Postar um comentário